- క్లోజ్డ్ సర్క్యూట్ కోసం
- ప్రత్యేక విభాగం మరియు పూర్తి ఎలక్ట్రికల్ సర్క్యూట్
- ఎలక్ట్రికల్ సర్క్యూట్ యొక్క ప్రస్తుత విభాగం యొక్క గణన
- పూర్తి గొలుసు కోసం గణన ఎంపిక
- వేరియబుల్పై చట్టం ప్రభావం
- పూర్తి సర్క్యూట్లో EMF మూలం
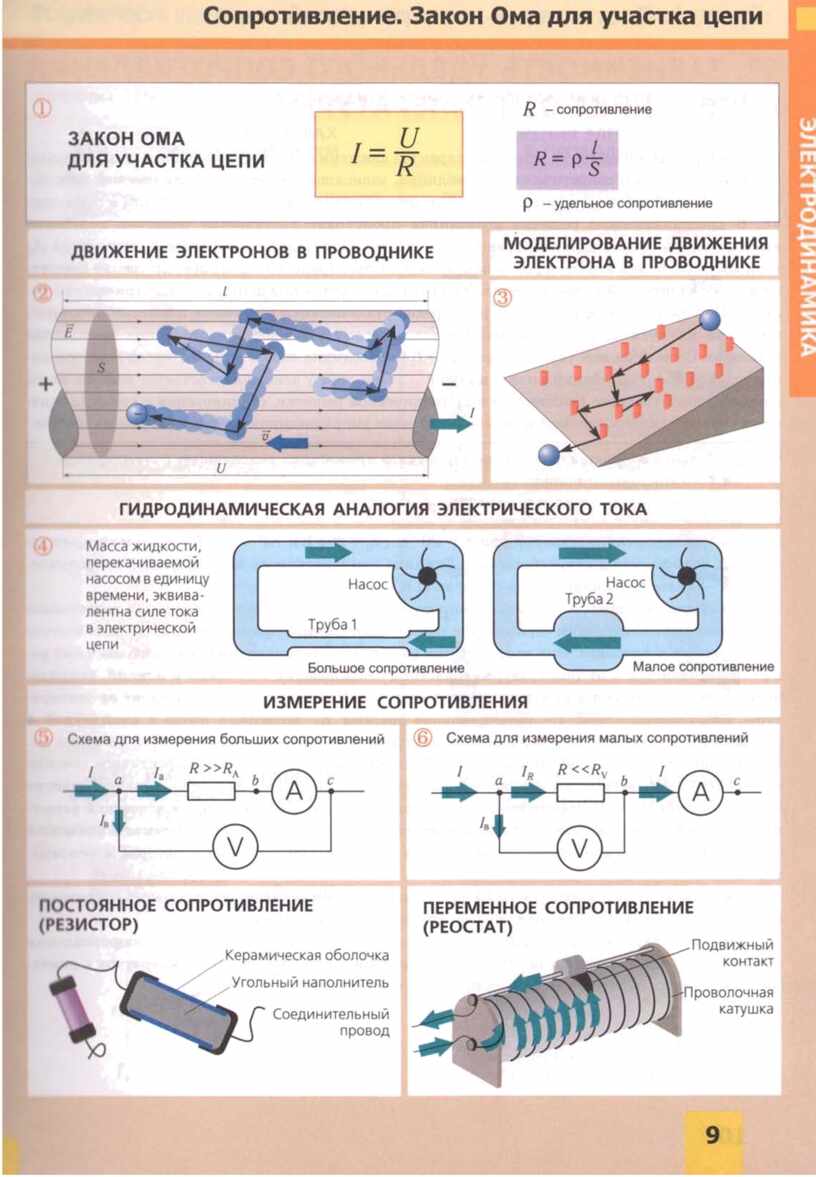
- R - విద్యుత్ నిరోధకత
- DC సర్క్యూట్ యొక్క నాన్-యూనిఫాం విభాగం
- మూలకాల యొక్క సీరియల్ మరియు సమాంతర కనెక్షన్
- సిరీస్-కనెక్ట్ చేయబడిన రెసిస్టివ్ ఎలిమెంట్స్ యొక్క గొలుసు
- సమాంతరంగా అనుసంధానించబడిన రెసిస్టివ్ మూలకాల గొలుసు
- చట్టం యొక్క సమగ్ర మరియు అవకలన రూపాలు
- కరెంట్ మరియు రెసిస్టెన్స్ని అర్థం చేసుకోవడం
- ఆల్టర్నేటింగ్ కరెంట్ కోసం ఓం యొక్క చట్టం
- ఓం యొక్క చట్టం సంభవించినప్పుడు
- కిర్చోఫ్ యొక్క చట్టాలు.
- ప్రాథమిక భావనలు
- బలం మరియు ఉద్రిక్తత
- కండక్టర్ నిరోధకత
- ఓం యొక్క చట్టం యొక్క వివరణ
- సమాంతర మరియు సీరియల్ కనెక్షన్
- సీరియల్ కనెక్షన్
- సమాంతర కనెక్షన్
- మనకు సమాంతర మరియు సీరియల్ కనెక్షన్ని ఏది ఇస్తుంది?
- ఆదర్శ EMF మూలం
- అవకలన రూపంలో
క్లోజ్డ్ సర్క్యూట్ కోసం
క్లోజ్డ్ సర్క్యూట్ అంటే క్లోజ్డ్ ఎలక్ట్రికల్ కనెక్షన్, దీని ద్వారా కరెంట్ ప్రసరిస్తుంది. ఒకదానికొకటి కనెక్ట్ అయ్యే వైర్ల శ్రేణి ఉన్నప్పుడు మరియు సర్క్యూట్ను పూర్తి చేయడం వలన నేను సర్కిల్ యొక్క ఒక చివర నుండి మరొక వైపుకు పరిగెత్తాను, అది క్లోజ్డ్ సర్క్యూట్ అవుతుంది.
EMF (E) - వోల్ట్లలో సూచించబడుతుంది మరియు కొలవబడుతుంది మరియు ఫెరడే చట్టం ప్రకారం బ్యాటరీ లేదా అయస్కాంత శక్తి ద్వారా ఉత్పన్నమయ్యే వోల్టేజ్ను సూచిస్తుంది, ఇది సమయం మారుతున్న అయస్కాంత క్షేత్రం విద్యుత్ ప్రవాహాన్ని ప్రేరేపిస్తుందని పేర్కొంది.
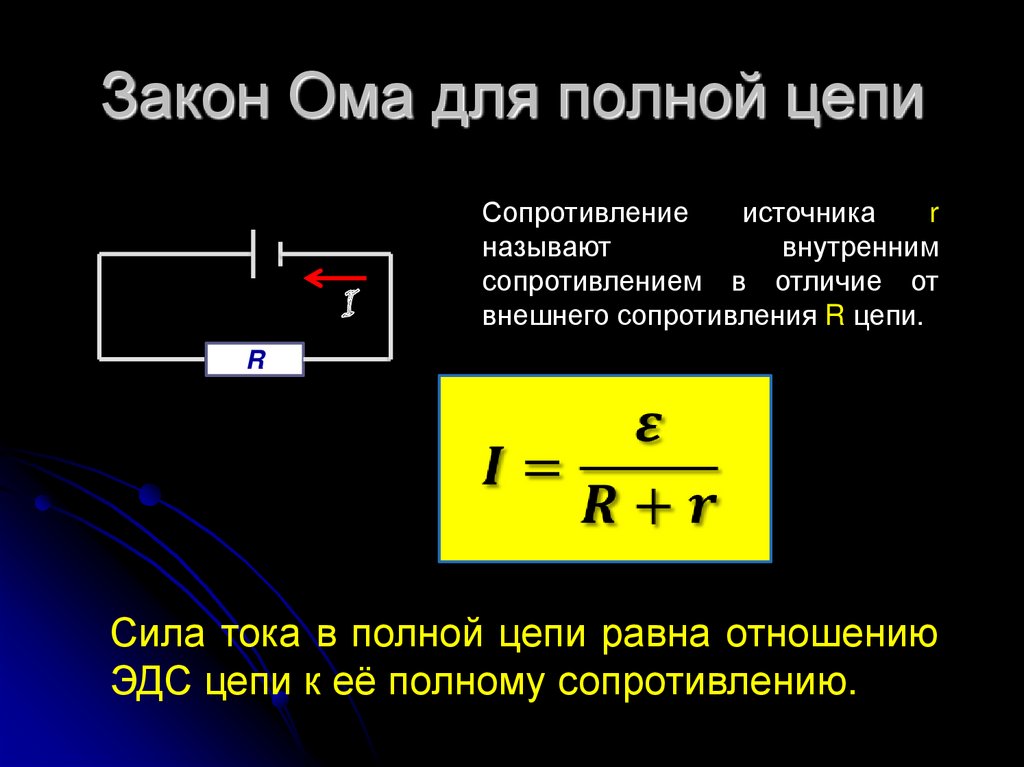
అప్పుడు: E = IR + Ir
E \u003d I (R + r)
I \u003d E / (R + r)
ఎక్కడ: r అనేది ప్రస్తుత మూలం యొక్క ప్రతిఘటన.
ఈ వ్యక్తీకరణను ఓం యొక్క క్లోజ్డ్ లూప్ సర్క్యూట్స్ లా అంటారు.
విజాతీయ గొలుసు
ప్రత్యేక విభాగం మరియు పూర్తి ఎలక్ట్రికల్ సర్క్యూట్
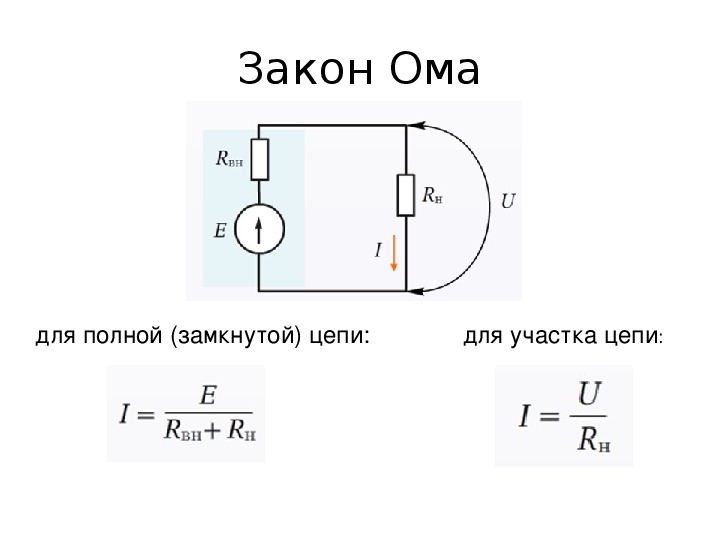
ఓం యొక్క చట్టం, ఒక విభాగానికి లేదా మొత్తం సర్క్యూట్కు వర్తించే విధంగా, రెండు గణన ఎంపికలలో పరిగణించబడుతుంది:
- ప్రత్యేక చిన్న విభాగం. ఇది EMF మూలం లేని సర్క్యూట్లో భాగం.
- ఒకటి లేదా అంతకంటే ఎక్కువ విభాగాలతో కూడిన పూర్తి గొలుసు. ఇది దాని స్వంత అంతర్గత ప్రతిఘటనతో EMF మూలాన్ని కూడా కలిగి ఉంటుంది.
ఎలక్ట్రికల్ సర్క్యూట్ యొక్క ప్రస్తుత విభాగం యొక్క గణన
ఈ సందర్భంలో, ప్రాథమిక సూత్రం I \u003d U / R వర్తించబడుతుంది, దీనిలో I ప్రస్తుత బలం, U అనేది వోల్టేజ్, R అనేది ప్రతిఘటన. దాని ప్రకారం, ఓం యొక్క చట్టం యొక్క సాధారణంగా ఆమోదించబడిన వివరణను రూపొందించవచ్చు:
గ్రాఫిక్ డిజైన్లో "చమోమిలే" అని పిలవబడే అనేక ఇతర సూత్రాలకు ఈ సూత్రీకరణ ఆధారం. సెక్టార్ P లో - శక్తి నిర్ణయించబడుతుంది, I, U మరియు R రంగాలలో - ప్రస్తుత బలం, వోల్టేజ్ మరియు నిరోధకతకు సంబంధించిన చర్యలు నిర్వహించబడతాయి.
ప్రతి వ్యక్తీకరణ - ప్రాథమిక మరియు అదనపు రెండూ, సర్క్యూట్లో ఉపయోగం కోసం ఉద్దేశించిన మూలకాల యొక్క ఖచ్చితమైన పారామితులను లెక్కించడానికి మిమ్మల్ని అనుమతిస్తుంది.
ఎలక్ట్రికల్ సర్క్యూట్లతో పనిచేసే నిపుణులు చిత్రంలో చూపిన త్రిభుజ పద్ధతిని ఉపయోగించి ఏదైనా పారామితుల యొక్క శీఘ్ర నిర్ణయాన్ని నిర్వహిస్తారు.
గణనలు విభాగం యొక్క మూలకాలను అనుసంధానించే కండక్టర్ల నిరోధకతను పరిగణనలోకి తీసుకోవాలి. అవి వేర్వేరు పదార్థాల నుండి తయారు చేయబడినందున, ఈ పరామితి ప్రతి సందర్భంలోనూ భిన్నంగా ఉంటుంది.పూర్తి సర్క్యూట్ను రూపొందించడం అవసరమైతే, ప్రధాన సూత్రం వోల్టేజ్ మూలం యొక్క పారామితులతో అనుబంధంగా ఉంటుంది, ఉదాహరణకు, బ్యాటరీ.
పూర్తి గొలుసు కోసం గణన ఎంపిక
ఒక పూర్తి సర్క్యూట్ అనేది ఒక వోల్టేజ్ మూలం (EMF)తో కలిపి ఒకే మొత్తంలో వ్యక్తిగత విభాగాలను కలిగి ఉంటుంది. అందువలన, విభాగాల యొక్క ఇప్పటికే ఉన్న ప్రతిఘటన కనెక్ట్ చేయబడిన మూలం యొక్క అంతర్గత నిరోధం ద్వారా భర్తీ చేయబడుతుంది. అందువల్ల, ముందుగా చర్చించబడిన ప్రధాన వివరణ క్రింది విధంగా చదవబడుతుంది: I = U / (R + r). ఇక్కడ, EMF మూలం యొక్క రెసిస్టివ్ ఇండికేటర్ (r) ఇప్పటికే జోడించబడింది.
స్వచ్ఛమైన భౌతిక శాస్త్రం యొక్క కోణం నుండి, ఈ సూచిక చాలా చిన్న విలువగా పరిగణించబడుతుంది. అయినప్పటికీ, ఆచరణలో, సంక్లిష్ట సర్క్యూట్లు మరియు సర్క్యూట్లను లెక్కించేటప్పుడు, నిపుణులు దానిని పరిగణనలోకి తీసుకోవలసి వస్తుంది, ఎందుకంటే అదనపు ప్రతిఘటన పని యొక్క ఖచ్చితత్వాన్ని ప్రభావితం చేస్తుంది. అదనంగా, ప్రతి మూలం యొక్క నిర్మాణం చాలా భిన్నమైనది, ఫలితంగా, కొన్ని సందర్భాల్లో నిరోధకత చాలా ఎక్కువ రేట్లు ద్వారా వ్యక్తీకరించబడుతుంది.
పైన పేర్కొన్న లెక్కలు DC సర్క్యూట్లకు సంబంధించి నిర్వహించబడతాయి. ప్రత్యామ్నాయ ప్రవాహంతో చర్యలు మరియు గణనలు వేరొక పథకం ప్రకారం తయారు చేయబడతాయి.
వేరియబుల్పై చట్టం ప్రభావం
ఆల్టర్నేటింగ్ కరెంట్తో, సర్క్యూట్ యొక్క ప్రతిఘటన అనేది ఇంపెడెన్స్ అని పిలవబడేది, ఇందులో యాక్టివ్ రెసిస్టెన్స్ మరియు రియాక్టివ్ రెసిస్టివ్ లోడ్ ఉంటుంది. ప్రేరక లక్షణాలు మరియు సైనూసోయిడల్ కరెంట్ విలువ కలిగిన మూలకాల ఉనికి దీనికి కారణం. వోల్టేజ్ కూడా ఒక వేరియబుల్, దాని స్వంత స్విచ్చింగ్ చట్టాల ప్రకారం పనిచేస్తుంది.
అందువల్ల, ఓం యొక్క చట్టం ప్రకారం ఒక AC సర్క్యూట్ నిర్దిష్ట ప్రభావాలను పరిగణనలోకి తీసుకుని లెక్కించబడుతుంది: వోల్టేజ్ నుండి కరెంట్ యొక్క పరిమాణాన్ని ప్రముఖంగా లేదా వెనుకబడి, అలాగే క్రియాశీల మరియు రియాక్టివ్ పవర్ ఉనికిని కలిగి ఉంటుంది.ప్రతిగా, ప్రతిచర్యలో ప్రేరక లేదా కెపాసిటివ్ భాగాలు ఉంటాయి.
ఈ దృగ్విషయాలన్నీ Z \u003d U / I లేదా Z \u003d R + J * (XL - XC) సూత్రానికి అనుగుణంగా ఉంటాయి, దీనిలో Z అనేది ఇంపెడెన్స్; R - క్రియాశీల లోడ్; XL, XC - ప్రేరక మరియు కెపాసిటివ్ లోడ్లు; J అనేది దిద్దుబాటు కారకం.
పూర్తి సర్క్యూట్లో EMF మూలం
ఒక క్లోజ్డ్ సర్క్యూట్లో ఎలక్ట్రిక్ కరెంట్ సంభవించడానికి, ఈ సర్క్యూట్ కనీసం ఒక ప్రత్యేక మూలకాన్ని కలిగి ఉండాలి, దీనిలో దాని ధ్రువాల మధ్య ఛార్జీలను బదిలీ చేసే పని జరుగుతుంది. ఈ మూలకం లోపల ఛార్జీలను మోసే శక్తులు విద్యుత్ క్షేత్రానికి వ్యతిరేకంగా అలా చేస్తాయి, అంటే వాటి స్వభావం విద్యుత్ నుండి భిన్నంగా ఉండాలి. అందువల్ల, అటువంటి శక్తులను మూడవ పక్షం అంటారు.
అన్నం. 1. భౌతిక శాస్త్రంలో బాహ్య శక్తులు.
ఎలక్ట్రికల్ ఫీల్డ్ యొక్క చర్యకు వ్యతిరేకంగా ఛార్జీలను బదిలీ చేయడానికి బాహ్య శక్తులు పని చేసే ఎలక్ట్రికల్ సర్క్యూట్ యొక్క మూలకాన్ని ప్రస్తుత మూలం అంటారు. దీని ప్రధాన లక్షణం బాహ్య శక్తుల పరిమాణం. దానిని వర్గీకరించడానికి, ఒక ప్రత్యేక కొలత ప్రవేశపెట్టబడింది - ఎలక్ట్రోమోటివ్ ఫోర్స్ (EMF), ఇది $\mathscr{E}$ అక్షరంతో సూచించబడుతుంది.
ప్రస్తుత మూలం యొక్క EMF విలువ ఈ ఛార్జ్ విలువకు ఛార్జ్ బదిలీ కోసం బాహ్య శక్తుల నిష్పత్తికి సమానంగా ఉంటుంది:
$$\mathscr{E}={A_{st}\over q}$$
EMF యొక్క అర్థం ఎలక్ట్రికల్ వోల్టేజ్ యొక్క అర్థానికి చాలా దగ్గరగా ఉన్నందున (రీకాల్, వోల్టేజ్ అనేది ఈ ఛార్జ్ యొక్క విలువకు ఛార్జ్ను కలిగి ఉన్న విద్యుత్ క్షేత్రం చేసే పని యొక్క నిష్పత్తి), అప్పుడు వోల్టేజ్ వంటి EMF కొలుస్తారు వోల్ట్లు:
$$1B={J\overCl}$$
నిజమైన ప్రస్తుత మూలం యొక్క రెండవ అతి ముఖ్యమైన విద్యుత్ లక్షణం దాని అంతర్గత నిరోధకత.టెర్మినల్స్ మధ్య ఛార్జీలు బదిలీ చేయబడినప్పుడు, అవి EMF మూలం యొక్క పదార్ధంతో సంకర్షణ చెందుతాయి మరియు అందువల్ల, విద్యుత్ ప్రవాహానికి మూలం కూడా కొంత నిరోధకతను అందిస్తుంది. అంతర్గత ప్రతిఘటన, సాధారణ ప్రతిఘటన వలె, ఓంలలో కొలుస్తారు, కానీ చిన్న లాటిన్ అక్షరం $r$ ద్వారా సూచించబడుతుంది.

అన్నం. 2. ప్రస్తుత మూలాల ఉదాహరణలు.
R - విద్యుత్ నిరోధకత
ప్రతిఘటన అనేది వోల్టేజ్ యొక్క పరస్పరం మరియు నడుస్తున్న నీటిలో కదలికకు వ్యతిరేకంగా శరీరాన్ని కదిలించే ప్రభావంతో పోల్చవచ్చు. R యొక్క యూనిట్ ఓం, ఇది పెద్ద గ్రీకు అక్షరం ఒమేగాతో సూచించబడుతుంది.
రెసిప్రోకల్ ఆఫ్ రెసిస్టెన్స్ (1/R)ని వాహకత అంటారు, ఇది సిమెన్స్ యూనిట్లలో వ్యక్తీకరించబడిన చార్జ్ని నిర్వహించే ఒక వస్తువు సామర్థ్యాన్ని కొలుస్తుంది.
ఉపయోగించిన రేఖాగణిత స్వతంత్ర పరిమాణాన్ని రెసిస్టివిటీ అని పిలుస్తారు మరియు సాధారణంగా గ్రీకు చిహ్నం r ద్వారా సూచించబడుతుంది.
అదనపు సమాచారం. ఓం యొక్క చట్టం విద్యుత్ నెట్వర్క్ యొక్క ఆపరేషన్ యొక్క మూడు ముఖ్యమైన సూచికలను స్థాపించడానికి సహాయపడుతుంది, ఇది శక్తి యొక్క గణనను సులభతరం చేస్తుంది. డయోడ్, ట్రాన్సిస్టర్ మరియు వంటి అంశాలతో ఒక-వైపు నెట్వర్క్లకు ఇది వర్తించదు. మరియు ఇది నాన్-లీనియర్ మూలకాలకు వర్తించదు, వీటిలో థైరిస్టర్లు ఉదాహరణలు, ఎందుకంటే ఈ మూలకాల యొక్క నిరోధక విలువ వేర్వేరు ఇచ్చిన వోల్టేజ్ మరియు కరెంట్తో మారుతుంది.
అధిక పౌనఃపున్యాల వద్ద, పంపిణీ ప్రవర్తన ప్రబలంగా మారుతుంది. చాలా పొడవైన విద్యుత్ లైన్ల విషయంలో కూడా అదే జరుగుతుంది. 60 Hz కంటే తక్కువ పౌనఃపున్యం వద్ద కూడా, 30 కిమీల వంటి చాలా పొడవైన ట్రాన్స్మిషన్ లైన్ పంపిణీ చేయబడిన స్వభావాన్ని కలిగి ఉంటుంది.ప్రధాన కారణం ఏమిటంటే, సర్క్యూట్లలో ప్రచారం చేసే ప్రభావవంతమైన విద్యుత్ సంకేతాలు విద్యుదయస్కాంత తరంగాలు, వోల్ట్లు మరియు ఆంపియర్లు కాదు, ఇవి విద్యుదయస్కాంత తరంగం ద్వారా సంక్రమిస్తాయి. కండక్టర్లు కేవలం తరంగాలకు మార్గదర్శకాలుగా పనిచేస్తాయి. కాబట్టి, ఉదాహరణకు, ఒక ఏకాక్షక కేబుల్ Z = 75 ఓమ్లను చూపుతుంది, దాని DC నిరోధకత చాలా తక్కువగా ఉన్నప్పటికీ.
ఓంస్ చట్టం అనేది ఎలక్ట్రికల్ ఇంజనీరింగ్ యొక్క ప్రాథమిక నియమం. ఇది అన్ని ఎలక్ట్రికల్ సర్క్యూట్లు మరియు ఎలక్ట్రానిక్ భాగాలలో పెద్ద సంఖ్యలో ఆచరణాత్మక అనువర్తనాలను కలిగి ఉంది.
ఓం యొక్క చట్టం యొక్క అప్లికేషన్ యొక్క అత్యంత సాధారణ ఉదాహరణలు:
- విద్యుత్ హీటర్కు విద్యుత్ సరఫరా చేయబడింది. హీటర్ కాయిల్ యొక్క నిరోధకత మరియు అనువర్తిత వోల్టేజీని బట్టి, ఆ హీటర్కు సరఫరా చేయబడిన శక్తిని లెక్కించవచ్చు.
- ఫ్యూజుల ఎంపిక. అవి ఎలక్ట్రానిక్ పరికరాలతో సిరీస్లో అనుసంధానించబడిన రక్షణ భాగాలు. ఫ్యూజ్లు/CBలు ఆంప్స్లో రేట్ చేయబడతాయి. ప్రస్తుత ఫ్యూజ్ రేటింగ్ ఓం నియమాన్ని ఉపయోగించి లెక్కించబడుతుంది.
- ఎలక్ట్రానిక్ పరికరాల రూపకల్పన. ల్యాప్టాప్లు మరియు మొబైల్ ఫోన్ల వంటి ఎలక్ట్రానిక్ పరికరాలకు నిర్దిష్ట ప్రస్తుత రేటింగ్తో కూడిన DC విద్యుత్ సరఫరా అవసరం. సాధారణ మొబైల్ ఫోన్ బ్యాటరీలకు 0.7-1A అవసరం. ఈ భాగాల ద్వారా ప్రవహించే కరెంట్ రేటును నియంత్రించడానికి రెసిస్టర్ ఉపయోగించబడుతుంది. ఓం యొక్క చట్టం సాధారణ సర్క్యూట్లో రేట్ చేయబడిన కరెంట్ను లెక్కించడానికి ఉపయోగించబడుతుంది.
ఒక సమయంలో, ఓమ్ యొక్క తీర్మానాలు విద్యుత్ రంగంలో కొత్త పరిశోధనలకు ఉత్ప్రేరకంగా మారాయి మరియు నేడు అవి వాటి ప్రాముఖ్యతను కోల్పోలేదు, ఎందుకంటే ఆధునిక ఎలక్ట్రికల్ ఇంజనీరింగ్ వాటిపై ఆధారపడి ఉంటుంది. 1841లో, ఓంకు రాయల్ సొసైటీ యొక్క అత్యున్నత గౌరవం, కోప్లీ మెడల్ లభించింది మరియు "ఓం" అనే పదం 1872లోనే ప్రతిఘటన యూనిట్గా గుర్తించబడింది.
DC సర్క్యూట్ యొక్క నాన్-యూనిఫాం విభాగం
ఒక భిన్నమైన నిర్మాణం సర్క్యూట్ యొక్క అటువంటి విభాగాన్ని కలిగి ఉంటుంది, ఇక్కడ, కండక్టర్లు మరియు మూలకాలతో పాటు, ప్రస్తుత మూలం ఉంది. ఈ ప్రాంతంలో మొత్తం ప్రస్తుత బలాన్ని లెక్కించేటప్పుడు దాని EMF తప్పనిసరిగా పరిగణనలోకి తీసుకోవాలి.
వైవిధ్యమైన సైట్ యొక్క ప్రధాన పారామితులు మరియు ప్రక్రియలను నిర్వచించే ఫార్ములా ఉంది: q = q0 x n x V. దాని సూచికలు క్రింది విధంగా వర్గీకరించబడతాయి:
- కదిలే ఛార్జీల ప్రక్రియలో (q), అవి నిర్దిష్ట సాంద్రతను పొందుతాయి. దీని పనితీరు ప్రస్తుత బలం మరియు కండక్టర్ (S) యొక్క క్రాస్ సెక్షనల్ ప్రాంతంపై ఆధారపడి ఉంటుంది.
- నిర్దిష్ట ఏకాగ్రత (n) పరిస్థితులలో, ఒకే వ్యవధిలో తరలించబడిన యూనిట్ ఛార్జీల (q0) సంఖ్యను ఖచ్చితంగా సూచించడం సాధ్యమవుతుంది.
- గణనల కోసం, కండక్టర్ షరతులతో కొంత వాల్యూమ్ (V) తో స్థూపాకార విభాగంగా పరిగణించబడుతుంది.
కండక్టర్ను బ్యాటరీకి కనెక్ట్ చేసినప్పుడు, తరువాతి కొంతకాలం తర్వాత డిస్చార్జ్ చేయబడుతుంది. అంటే, ఎలక్ట్రాన్ల కదలిక క్రమంగా మందగిస్తుంది మరియు చివరికి, పూర్తిగా ఆగిపోతుంది. ఇది కండక్టర్ యొక్క మాలిక్యులర్ లాటిస్ ద్వారా సులభతరం చేయబడుతుంది, ఇది ఒకదానికొకటి మరియు ఇతర కారకాలతో ఎలక్ట్రాన్ల తాకిడిని ప్రతిఘటిస్తుంది. అటువంటి ప్రతిఘటనను అధిగమించడానికి, నిర్దిష్ట థర్డ్-పార్టీ బలగాలను అదనంగా వర్తింపజేయాలి.
లెక్కల సమయంలో, ఈ శక్తులు కూలంబ్ వాటికి జోడించబడతాయి. అదనంగా, 1వ పాయింట్ నుండి 2వ పాయింట్కి యూనిట్ ఛార్జ్ qని బదిలీ చేయడానికి, A1-2 లేదా కేవలం A12 పనిని నిర్వహించడం అవసరం. ఈ ప్రయోజనం కోసం, సంభావ్య వ్యత్యాసం (ϕ1 - ϕ2) సృష్టించబడుతుంది. డైరెక్ట్ కరెంట్ సోర్స్ యొక్క చర్యలో, ఒక EMF పుడుతుంది, సర్క్యూట్ వెంట ఛార్జీలను కదిలిస్తుంది. మొత్తం ఒత్తిడి యొక్క పరిమాణం పైన పేర్కొన్న అన్ని శక్తులను కలిగి ఉంటుంది.
DC సరఫరాకు కనెక్షన్ యొక్క ధ్రువణత తప్పనిసరిగా గణనలలో పరిగణనలోకి తీసుకోవాలి. టెర్మినల్స్ మార్చబడినప్పుడు, EMF కూడా మారుతుంది, ఛార్జీల కదలికను వేగవంతం చేస్తుంది లేదా నెమ్మదిస్తుంది.
మూలకాల యొక్క సీరియల్ మరియు సమాంతర కనెక్షన్
ఎలక్ట్రికల్ సర్క్యూట్ (సర్క్యూట్ యొక్క విభాగం) యొక్క మూలకాల కోసం, ఒక లక్షణం క్షణం అనేది సిరీస్ లేదా సమాంతర కనెక్షన్.
దీని ప్రకారం, ప్రతి రకమైన కనెక్షన్ ప్రస్తుత ప్రవాహం మరియు వోల్టేజ్ సరఫరా యొక్క విభిన్న స్వభావంతో కూడి ఉంటుంది. ఈ ఖాతాలో, మూలకాలను చేర్చే ఎంపికపై ఆధారపడి, ఓం యొక్క చట్టం కూడా వివిధ మార్గాల్లో వర్తించబడుతుంది.
సిరీస్-కనెక్ట్ చేయబడిన రెసిస్టివ్ ఎలిమెంట్స్ యొక్క గొలుసు
సిరీస్ కనెక్షన్కి సంబంధించి (రెండు భాగాలతో సర్క్యూట్ యొక్క విభాగం), పదాలు ఉపయోగించబడుతుంది:
- నేను = నేను1 = నేను2 ;
- యు = యు1 + యు2 ;
- R=R1 + ఆర్2
సిరీస్లో అనుసంధానించబడిన రెసిస్టివ్ భాగాల సంఖ్యతో సంబంధం లేకుండా, సర్క్యూట్లోని ఒక విభాగంలో ప్రవహించే కరెంట్ విలువను మార్చదని ఈ సూత్రీకరణ స్పష్టంగా చూపిస్తుంది.
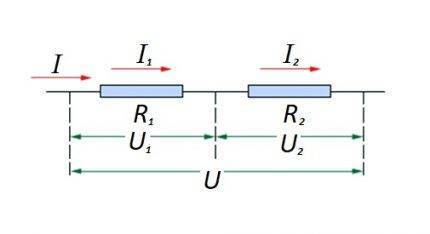 ఒకదానితో ఒకటి సిరీస్లో సర్క్యూట్ విభాగంలో రెసిస్టివ్ ఎలిమెంట్లను కనెక్ట్ చేయడం. ఈ ఎంపికకు దాని స్వంత గణన చట్టం ఉంది. రేఖాచిత్రంలో: I, I1, I2 - ప్రస్తుత ప్రవాహం; R1, R2 - నిరోధక అంశాలు; U, U1, U2 - దరఖాస్తు వోల్టేజ్
ఒకదానితో ఒకటి సిరీస్లో సర్క్యూట్ విభాగంలో రెసిస్టివ్ ఎలిమెంట్లను కనెక్ట్ చేయడం. ఈ ఎంపికకు దాని స్వంత గణన చట్టం ఉంది. రేఖాచిత్రంలో: I, I1, I2 - ప్రస్తుత ప్రవాహం; R1, R2 - నిరోధక అంశాలు; U, U1, U2 - దరఖాస్తు వోల్టేజ్
సర్క్యూట్ యొక్క క్రియాశీల రెసిస్టివ్ భాగాలకు వర్తించే వోల్టేజ్ మొత్తం మొత్తం మరియు EMF మూలం యొక్క విలువకు జోడిస్తుంది.
ఈ సందర్భంలో, ప్రతి వ్యక్తిగత భాగంపై వోల్టేజ్: Ux = I * Rx.
మొత్తం ప్రతిఘటనను సర్క్యూట్ యొక్క అన్ని రెసిస్టివ్ భాగాల విలువల మొత్తంగా పరిగణించాలి.
సమాంతరంగా అనుసంధానించబడిన రెసిస్టివ్ మూలకాల గొలుసు
రెసిస్టివ్ భాగాల సమాంతర కనెక్షన్ ఉన్న సందర్భంలో, జర్మన్ భౌతిక శాస్త్రవేత్త ఓం యొక్క చట్టానికి సంబంధించి సూత్రీకరణ న్యాయమైనదిగా పరిగణించబడుతుంది:
- నేను = నేను1 + ఐ2 … ;
- యు = యు1 = యు2 … ;
- 1/R = 1/R1 + 1 / ఆర్2 + …
సమాంతర మరియు సీరియల్ కనెక్షన్లను ఉపయోగించినప్పుడు "మిశ్రమ" రకం యొక్క సర్క్యూట్ విభాగాలను కంపైల్ చేయడానికి ఎంపికలు మినహాయించబడవు.
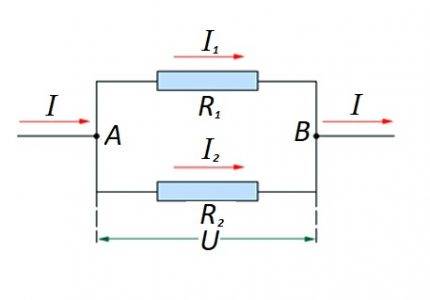 ఒకదానితో ఒకటి సమాంతరంగా సర్క్యూట్ విభాగంలో రెసిస్టివ్ ఎలిమెంట్స్ యొక్క కనెక్షన్. ఈ ఎంపిక కోసం, దాని స్వంత గణన చట్టం వర్తించబడుతుంది. రేఖాచిత్రంలో: I, I1, I2 - ప్రస్తుత ప్రవాహం; R1, R2 - నిరోధక అంశాలు; U - దరఖాస్తు వోల్టేజ్; A, B - ప్రవేశ / నిష్క్రమణ పాయింట్లు
ఒకదానితో ఒకటి సమాంతరంగా సర్క్యూట్ విభాగంలో రెసిస్టివ్ ఎలిమెంట్స్ యొక్క కనెక్షన్. ఈ ఎంపిక కోసం, దాని స్వంత గణన చట్టం వర్తించబడుతుంది. రేఖాచిత్రంలో: I, I1, I2 - ప్రస్తుత ప్రవాహం; R1, R2 - నిరోధక అంశాలు; U - దరఖాస్తు వోల్టేజ్; A, B - ప్రవేశ / నిష్క్రమణ పాయింట్లు
అటువంటి ఎంపికల కోసం, గణన సాధారణంగా సమాంతర కనెక్షన్ యొక్క రెసిస్టివ్ రేటింగ్ యొక్క ప్రారంభ గణన ద్వారా నిర్వహించబడుతుంది. అప్పుడు సిరీస్లో కనెక్ట్ చేయబడిన రెసిస్టర్ యొక్క విలువ ఫలితానికి జోడించబడుతుంది.
చట్టం యొక్క సమగ్ర మరియు అవకలన రూపాలు
గణనలతో పైన పేర్కొన్న అన్ని పాయింట్లు "సజాతీయ" నిర్మాణం యొక్క కండక్టర్లను ఎలక్ట్రికల్ సర్క్యూట్లలో భాగంగా ఉపయోగించినప్పుడు పరిస్థితులకు వర్తిస్తాయి.
ఇంతలో, ఆచరణలో, ఒక స్కీమాటిక్ నిర్మాణాన్ని తరచుగా ఎదుర్కోవలసి ఉంటుంది, ఇక్కడ కండక్టర్ల నిర్మాణం వివిధ ప్రాంతాల్లో మారుతుంది. ఉదాహరణకు, ఒక పెద్ద క్రాస్ సెక్షన్ యొక్క వైర్లు ఉపయోగించబడతాయి లేదా, దీనికి విరుద్ధంగా, చిన్నవి, వివిధ పదార్థాల ఆధారంగా తయారు చేయబడతాయి.
అటువంటి వ్యత్యాసాలను పరిగణనలోకి తీసుకోవడానికి, "అవకలన-సమగ్ర ఓం యొక్క చట్టం" అని పిలవబడే వైవిధ్యం ఉంది. అనంతమైన చిన్న కండక్టర్ కోసం, ప్రస్తుత సాంద్రత స్థాయి తీవ్రత మరియు వాహకత విలువపై ఆధారపడి లెక్కించబడుతుంది.
అవకలన గణన కింద, ఫార్ములా తీసుకోబడింది: J = ό * E
సమగ్ర గణన కోసం, వరుసగా, సూత్రీకరణ: I * R = φ1 - φ2 + έ
అయినప్పటికీ, ఈ ఉదాహరణలు ఉన్నత గణిత శాస్త్రానికి దగ్గరగా ఉంటాయి మరియు వాస్తవానికి సాధారణ ఎలక్ట్రీషియన్ యొక్క నిజమైన అభ్యాసంలో ఉపయోగించబడవు.
కరెంట్ మరియు రెసిస్టెన్స్ని అర్థం చేసుకోవడం
విద్యుత్ ప్రవాహ భావనతో ప్రారంభిద్దాం.సంక్షిప్తంగా, లోహాలకు సంబంధించి ఎలెక్ట్రిక్ కరెంట్ అనేది ఎలక్ట్రాన్ల నిర్దేశిత కదలిక - ప్రతికూలంగా చార్జ్ చేయబడిన కణాలు. అవి సాధారణంగా చిన్న వృత్తాలుగా సూచించబడతాయి. ప్రశాంతమైన స్థితిలో, వారు యాదృచ్ఛికంగా కదులుతారు, నిరంతరం వారి దిశను మారుస్తారు. కొన్ని పరిస్థితులలో - సంభావ్య వ్యత్యాసం యొక్క రూపాన్ని - ఈ కణాలు ఏదో ఒక దిశలో ఒక నిర్దిష్ట కదలికను ప్రారంభిస్తాయి. ఈ కదలిక విద్యుత్ ప్రవాహం.
దీన్ని మరింత స్పష్టంగా చేయడానికి, మనం ఎలక్ట్రాన్లను ఏదో ఒక విమానంలో చిందిన నీటితో పోల్చవచ్చు. విమానం నిశ్చలంగా ఉన్నంత కాలం నీరు కదలదు. కానీ, ఒక వాలు కనిపించిన వెంటనే (సంభావ్య వ్యత్యాసం తలెత్తింది), నీరు కదలడం ప్రారంభించింది. ఎలక్ట్రాన్ల విషయంలోనూ అంతే.
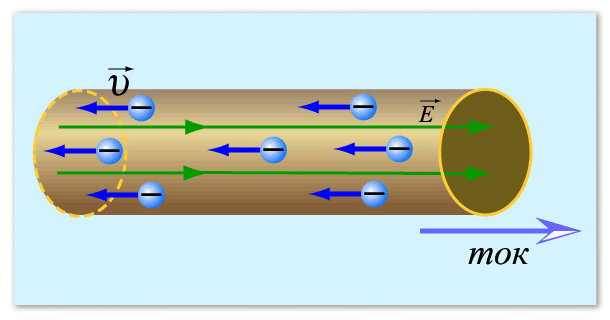
విద్యుత్ ప్రవాహాన్ని ఈ విధంగా ఊహించవచ్చు
ఇప్పుడు మనం ప్రతిఘటన అంటే ఏమిటో అర్థం చేసుకోవాలి మరియు వారు ప్రస్తుత బలంతో ఎందుకు అభిప్రాయాన్ని కలిగి ఉన్నారు: అధిక నిరోధకత, తక్కువ కరెంట్. మీకు తెలిసినట్లుగా, ఎలక్ట్రాన్లు కండక్టర్ ద్వారా కదులుతాయి. సాధారణంగా ఇవి మెటల్ వైర్లు, ఎందుకంటే లోహాలు విద్యుత్తును నిర్వహించగల మంచి సామర్థ్యాన్ని కలిగి ఉంటాయి. లోహానికి దట్టమైన క్రిస్టల్ లాటిస్ ఉందని మనకు తెలుసు: దగ్గరగా మరియు పరస్పరం అనుసంధానించబడిన అనేక కణాలు. ఎలక్ట్రాన్లు, లోహ పరమాణువుల మధ్య తమ మార్గాన్ని తయారు చేస్తాయి, వాటిని ఢీకొంటాయి, ఇది వాటిని కదలడానికి కష్టతరం చేస్తుంది. కండక్టర్ చేసే ప్రతిఘటనను వివరించడానికి ఇది సహాయపడుతుంది. ఎక్కువ ప్రతిఘటన, తక్కువ ప్రస్తుత బలం ఎందుకు ఇప్పుడు స్పష్టమవుతుంది - ఎక్కువ కణాలు, ఎలక్ట్రాన్లు మార్గాన్ని అధిగమించడం చాలా కష్టం, అవి నెమ్మదిగా చేస్తాయి. దీంతో సర్దుకుపోయినట్లు తెలుస్తోంది.
మీరు ఈ ఆధారపడటాన్ని అనుభవపూర్వకంగా పరీక్షించాలనే కోరిక ఉంటే, వేరియబుల్ రెసిస్టర్ను కనుగొనండి, సిరీస్లో రెసిస్టర్ను కనెక్ట్ చేయండి - ఒక అమ్మీటర్ - ప్రస్తుత మూలం (బ్యాటరీ).సర్క్యూట్లోకి స్విచ్ని చొప్పించడం కూడా అవసరం - ఒక సాధారణ టోగుల్ స్విచ్.
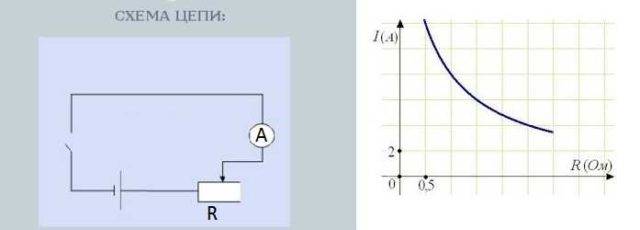
ప్రతిఘటనపై ప్రస్తుత ఆధారపడటాన్ని పరీక్షించడానికి సర్క్యూట్
రెసిస్టర్ నాబ్ను తిప్పడం వల్ల నిరోధం మారుతుంది. అదే సమయంలో, ప్రస్తుత బలాన్ని కొలిచే అమ్మీటర్లోని రీడింగులు కూడా మారుతాయి. అంతేకాకుండా, ఎక్కువ ప్రతిఘటన, తక్కువ బాణం విచలనం - తక్కువ ప్రస్తుత. తక్కువ ప్రతిఘటన, మరింత బాణం విచలనం - ప్రస్తుత ఎక్కువ.
ప్రతిఘటనపై కరెంట్ ఆధారపడటం దాదాపు సరళంగా ఉంటుంది, అనగా ఇది గ్రాఫ్లో దాదాపు సరళ రేఖగా ప్రతిబింబిస్తుంది. దాదాపు ఎందుకు - ఇది విడిగా చర్చించబడాలి, కానీ అది మరొక కథ.
ఆల్టర్నేటింగ్ కరెంట్ కోసం ఓం యొక్క చట్టం
AC సర్క్యూట్లను లెక్కించేటప్పుడు, ప్రతిఘటన భావనకు బదులుగా, "ఇంపెడెన్స్" అనే భావన పరిచయం చేయబడింది. ఇంపెడెన్స్ Z అక్షరంతో సూచించబడుతుంది, ఇది లోడ్ R యొక్క క్రియాశీల నిరోధకతను కలిగి ఉంటుందిa మరియు ప్రతిచర్య X (లేదా Rఆర్) ఇది సైనూసోయిడల్ కరెంట్ (మరియు ఏదైనా ఇతర రూపాల ప్రవాహాలు) మరియు ప్రేరక మూలకాల యొక్క పారామితులు, అలాగే మారే చట్టాల ఆకృతి కారణంగా ఉంటుంది:
- ఇండక్టివ్ సర్క్యూట్లోని కరెంట్ తక్షణమే మారదు.
- కెపాసిటెన్స్ ఉన్న సర్క్యూట్లోని వోల్టేజ్ తక్షణమే మారదు.
అందువలన, కరెంట్ లాగ్ లేదా వోల్టేజ్ని నడిపించడం ప్రారంభమవుతుంది, మరియు స్పష్టమైన శక్తి చురుకుగా మరియు రియాక్టివ్గా విభజించబడింది.
U=I/Z
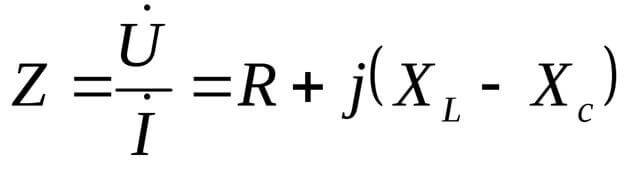
Xఎల్ మరియు Xసి లోడ్ యొక్క రియాక్టివ్ భాగాలు.
ఈ విషయంలో, విలువ cosФ పరిచయం చేయబడింది:
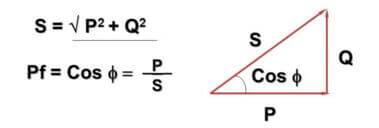
ఇక్కడ - Q - ఆల్టర్నేటింగ్ కరెంట్ మరియు ఇండక్టివ్-కెపాసిటివ్ కాంపోనెంట్స్ కారణంగా రియాక్టివ్ పవర్, P - యాక్టివ్ పవర్ (క్రియాశీల భాగాలలో వెదజల్లుతుంది), S - స్పష్టమైన శక్తి, cosФ - పవర్ ఫ్యాక్టర్.
ఫార్ములా మరియు దాని ప్రాతినిధ్యం పైథాగరియన్ సిద్ధాంతంతో కలుస్తుందని మీరు గమనించి ఉండవచ్చు. ఇది నిజం మరియు కోణం Ф లోడ్ యొక్క రియాక్టివ్ భాగం ఎంత పెద్దది అనే దానిపై ఆధారపడి ఉంటుంది - ఇది పెద్దది, పెద్దది.ఆచరణలో, ఇది వాస్తవానికి నెట్వర్క్లో ప్రవహించే కరెంట్ గృహ మీటర్ ద్వారా పరిగణనలోకి తీసుకున్న దానికంటే ఎక్కువగా ఉంటుంది, అయితే సంస్థలు పూర్తి శక్తి కోసం చెల్లిస్తాయి.
ఈ సందర్భంలో, ప్రతిఘటన సంక్లిష్ట రూపంలో ప్రదర్శించబడుతుంది:
ఇక్కడ j అనేది ఒక ఊహాత్మక యూనిట్, ఇది సమీకరణాల సంక్లిష్ట రూపానికి విలక్షణమైనది. తక్కువ సాధారణంగా i అని పిలుస్తారు, కానీ ఎలక్ట్రికల్ ఇంజనీరింగ్లో, ఆల్టర్నేటింగ్ కరెంట్ యొక్క ప్రభావవంతమైన విలువ కూడా సూచించబడుతుంది, కాబట్టి, గందరగోళం చెందకుండా ఉండటానికి, j ని ఉపయోగించడం మంచిది.
ఊహాత్మక యూనిట్ √-1. స్క్వేర్ చేసినప్పుడు అటువంటి సంఖ్య లేదని తార్కికంగా ఉంటుంది, ఇది "-1" యొక్క ప్రతికూల ఫలితానికి దారి తీస్తుంది.
ఓం యొక్క చట్టం సంభవించినప్పుడు
ఆదర్శ పరిస్థితులను సృష్టించడం సులభం కాదు. స్వచ్ఛమైన కండక్టర్లలో కూడా, విద్యుత్ నిరోధకత ఉష్ణోగ్రతతో మారుతుంది. దీని తగ్గుదల క్రిస్టల్ లాటిస్ యొక్క అణువుల కార్యకలాపాలను తగ్గిస్తుంది, ఇది ఉచిత ఛార్జీల కదలికను సులభతరం చేస్తుంది. "గడ్డకట్టడం" యొక్క నిర్దిష్ట స్థాయిలో సూపర్ కండక్టివిటీ ప్రభావం ఏర్పడుతుంది. వేడి చేసినప్పుడు వ్యతిరేక ప్రభావం (వాహకత క్షీణత) గమనించవచ్చు.
అదే సమయంలో, ఎలక్ట్రోలైట్లు, లోహాలు మరియు కొన్ని రకాల సిరమిక్స్ ప్రస్తుత సాంద్రతతో సంబంధం లేకుండా విద్యుత్ నిరోధకతను కలిగి ఉంటాయి. నిర్దిష్ట ఉష్ణోగ్రత పాలనను కొనసాగించేటప్పుడు పారామితుల స్థిరత్వం అదనపు దిద్దుబాట్లు లేకుండా ఓం యొక్క సూత్రాలను వర్తింపజేయడం సాధ్యం చేస్తుంది.
సెమీకండక్టర్ పదార్థాలు మరియు వాయువులు వివిధ విద్యుత్ నిరోధకత ద్వారా వర్గీకరించబడతాయి. ఈ పరామితి నియంత్రణ వాల్యూమ్లోని ప్రస్తుత తీవ్రత ద్వారా గణనీయంగా ప్రభావితమవుతుంది. పనితీరు లక్షణాలను లెక్కించడానికి, ప్రత్యేక గణన పద్ధతులను తప్పనిసరిగా వర్తింపజేయాలి.
ప్రత్యామ్నాయ ప్రవాహాన్ని పరిగణించినట్లయితే, గణన పద్ధతి సరిదిద్దబడింది.ఈ సందర్భంలో, రియాక్టివ్ భాగాల ఉనికిని పరిగణనలోకి తీసుకోవాలి. ప్రతిఘటన యొక్క నిరోధక స్వభావంతో, ఓం యొక్క సూత్రం యొక్క సూత్రాల ఆధారంగా పరిగణించబడే గణన సాంకేతికతలను వర్తింపజేయడం సాధ్యమవుతుంది.
కిర్చోఫ్ యొక్క చట్టాలు.
పంపిణీ
ఎలక్ట్రికల్ సర్క్యూట్ యొక్క శాఖలలో ప్రవాహాలు
కిర్చోఫ్ యొక్క మొదటి నియమాన్ని పాటిస్తుంది,
మరియు విభాగాలపై ఒత్తిడి పంపిణీ
గొలుసు కిర్చోఫ్ యొక్క రెండవ నియమాన్ని పాటిస్తుంది.
కిర్చోఫ్ యొక్క చట్టాలు
ఓం చట్టంతో పాటు ప్రధానమైనవి
ఎలక్ట్రికల్ సర్క్యూట్ల సిద్ధాంతంలో.
మొదటిది
కిర్చోఫ్ చట్టం:
బీజగణితం
నోడ్లోని ప్రవాహాల మొత్తం సున్నా:
i
= 0 (19)
ఎక్కడ
i
ఇచ్చిన నోడ్ వద్ద కలుస్తున్న శాఖల సంఖ్య.
అంటే సమ్మషన్
శాఖలలోని ప్రవాహాల వరకు విస్తరించింది,
పరిగణించబడిన వాటిలో కలుస్తాయి
నోడ్.
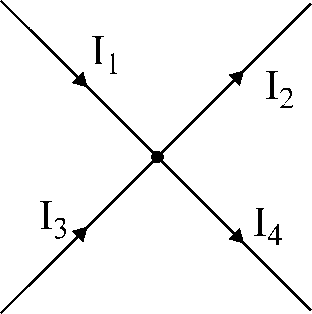
Fig.17. ఇలస్ట్రేషన్
కిర్చోఫ్ యొక్క మొదటి నియమానికి.
సంఖ్య
మొదటి ప్రకారం సంకలనం చేయబడిన సమీకరణాలు
కిర్చోఫ్ చట్టం సూత్రం ద్వారా నిర్ణయించబడుతుంది:
నూప్
= ను
– 1,
ఎక్కడ
ను
పరిగణించబడే గొలుసులోని నోడ్ల సంఖ్య.
ప్రవాహాల సంకేతాలు
ఎంచుకున్న వాటిని పరిగణనలోకి తీసుకొని సమీకరణాలు తీసుకోబడతాయి
సానుకూల దిశ. వద్ద సంకేతాలు
ప్రవాహాలు ఒకేలా ఉంటే ప్రవాహాలు ఒకే విధంగా ఉంటాయి
దీనికి సంబంధించి ఓరియెంటెడ్
నోడ్.
ఉదాహరణకి,
అంజీర్ 17లో చూపబడిన నోడ్ కోసం:
మేము నోడ్కు ప్రవహించే ప్రవాహాలకు సంకేతాలను కేటాయిస్తాము
"+", మరియు నోడ్ నుండి ప్రవహించే ప్రవాహాలకు - సంకేతాలు
«-».
అప్పుడు సమీకరణం
కిర్చోఫ్ యొక్క మొదటి చట్టం ప్రకారం, ఇది వ్రాయబడుతుంది
కాబట్టి:
I1
- ఐ2
+ ఐ3
- ఐ4
= 0.
సమీకరణాలు,
కిర్చోఫ్ యొక్క మొదటి చట్టం ప్రకారం సంకలనం చేయబడింది,
నోడ్స్ అంటారు.
ఈ
చట్టం నోడ్లో ఉన్న వాస్తవాన్ని వ్యక్తపరుస్తుంది
విద్యుత్ ఛార్జ్ పేరుకుపోదు
మరియు వినియోగించబడదు. విద్యుత్ మొత్తం
సైట్కు వచ్చే ఛార్జీలు మొత్తానికి సమానం
నోడ్ను ఒకదానిలో వదిలివేసే ఛార్జీలు
అదే వ్యవధి.
రెండవ
కిర్చోఫ్ చట్టం:
బీజగణితం
emf మొత్తం ఏదైనా క్లోజ్డ్ సర్క్యూట్లో
గొలుసు జలపాతం యొక్క బీజగణిత మొత్తానికి సమానం
ఈ సర్క్యూట్ మూలకాలపై వోల్టేజ్:
Ui
=
Ei
IiRi=Ei(20)
ఎక్కడ
i
- మూలకం సంఖ్య (నిరోధకత లేదా
వోల్టేజ్ మూలం) పరిగణించబడుతుంది
ఆకృతి.
**సంఖ్య
రెండవ ప్రకారం సంకలనం చేయబడిన సమీకరణాలు
కిర్చోఫ్ చట్టం సూత్రం ద్వారా నిర్ణయించబడుతుంది:
నూప్
= Nb
- ను
+ 1 – Ned.s.
ఎక్కడ
Nb
- ఎలక్ట్రికల్ సర్క్యూట్ యొక్క శాఖల సంఖ్య;
ను
- నోడ్స్ సంఖ్య;
Ned.s.
ఆదర్శ emf మూలాల సంఖ్య.
Fig.18. ఇలస్ట్రేషన్
కిర్చోఫ్ యొక్క రెండవ నియమానికి.
కోసం,
రెండవ చట్టాన్ని సరిగ్గా వ్రాయడానికి
ఇచ్చిన ఆకృతి కోసం Kirchhoff, అనుసరిస్తుంది
కింది నియమాలకు అనుగుణంగా:
-
ఏకపక్షంగా
కాంటౌర్ బైపాస్ దిశను ఎంచుకోండి,
ఉదాహరణకు, సవ్యదిశలో (Fig. 18). -
emf
మరియు వోల్టేజ్ తగ్గుతుంది
ఎంచుకున్న దిశతో దిశలో
బైపాస్ తో వ్యక్తీకరణలో వ్రాయబడ్డాయి
"+" గుర్తు; ఒకవేళ ఇ.ఎఫ్.ఎస్. మరియు వోల్టేజ్ డ్రాప్
దిశతో సరిపోలడం లేదు
ఆకృతి, అప్పుడు అవి ఒక గుర్తుతో ముందు ఉంటాయి
«-».
ఉదాహరణకి,
Fig. 18 యొక్క ఆకృతి కోసం, Kirchhoff రెండవ చట్టం
ఈ క్రింది విధంగా వ్రాయబడుతుంది:
యు1
- యు2
+ యు3
= ఇ1
- ఇ3
- ఇ4
(21)
సమీకరణం (20) కావచ్చు
ఇలా తిరిగి వ్రాయండి:
(Ui
– ఈ)
= 0 (22)
ఎక్కడ
(యు
– ఇ)
- శాఖపై ఉద్రిక్తత.
తత్ఫలితంగా,
కిర్చోఫ్ యొక్క రెండవ నియమాన్ని రూపొందించవచ్చు
కింది విధంగా:
బీజగణితం
ఏదైనా శాఖలలోని వోల్టేజీల మొత్తం
క్లోజ్డ్ లూప్ సున్నా.
సంభావ్య
ముందుగా చర్చించిన రేఖాచిత్రం పనిచేస్తుంది
రెండవ యొక్క గ్రాఫికల్ వివరణ
కిర్చోఫ్ చట్టం.
విధి సంఖ్య 1.
AT
అంజీర్ 1లోని సర్క్యూట్ I ప్రవాహాలు ఇవ్వబడింది1
మరియు నేను3,
ప్రతిఘటన మరియు emf ప్రవాహాలను నిర్ణయించండి
I4,
I5,
I6
; పాయింట్ల మధ్య వోల్టేజ్ a
మరియు బి
నేను ఉంటే1
= 10mA,
I3
= -20 mA,
ఆర్4
= 5kOhm,
ఇ5
= 20B,
ఆర్5
= 3kOhm,
ఇ6
= 40B,
ఆర్6
= 2kOhm.
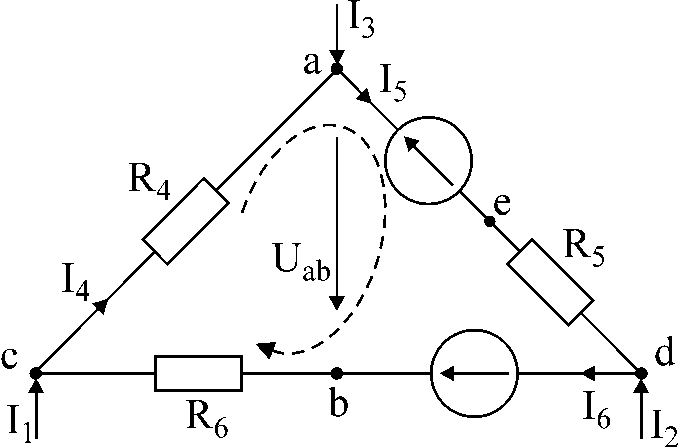
చిత్రం 1
పరిష్కారం:
-
ఇచ్చిన కోసం
ఆకృతి, మేము ప్రకారం రెండు సమీకరణాలను కంపోజ్ చేస్తాము
కిర్చోఫ్ యొక్క మొదటి చట్టం మరియు ఒకటి - ప్రకారం
రెండవ. ఆకృతి దిశ
బాణం ద్వారా సూచించబడింది.

AT
పరిష్కారం ఫలితంగా మనకు లభిస్తుంది: I6
= 0; I4
= 10mA;
I5
= -10mA
-
అడగండి
పాయింట్ల మధ్య వోల్టేజ్ దిశ
a
మరియు బి
పాయింట్ "a" నుండి
"బి"ని సూచించడానికి
- యుab.
ఈ వోల్టేజ్ సమీకరణం నుండి కనుగొనవచ్చు
కిర్చోఫ్ యొక్క రెండవ నియమం:
I4ఆర్4
+ యుab
+ ఐ6ఆర్6
= 0
యుab
= - 50V.
పని సంఖ్య 2.
కోసం
అంజీర్ 2లోని రేఖాచిత్రాలు ప్రకారం సమీకరణాలను రూపొందించండి
కిర్చోఫ్ యొక్క చట్టాలు మరియు తెలియని వాటిని నిర్ణయిస్తాయి
పాయింట్లు.
ఇచ్చిన:
I1
= 20mA;
I2
= 10mA
ఆర్1
= 5kOhm,
ఆర్3
= 4kOhm,
ఆర్4
= 6kOhm,
ఆర్5
= 2kOhm,
ఆర్6
= 4kΩ.
Fig.2
పరిష్కారం:
నోడ్ల సంఖ్య
సమీకరణాలు - 3, ఆకృతి సమీకరణాల సంఖ్య
– 1.
గుర్తుంచుకో!
రెండవ ప్రకారం సమీకరణాన్ని కంపైల్ చేస్తున్నప్పుడు
Kirchhoff చట్టం, మేము ఆకృతిని ఎంచుకుంటాము
ఇది ప్రస్తుత మూలాలను కలిగి ఉండదు.
ఆకృతి యొక్క దిశ చిత్రంలో సూచించబడింది.
AT
ఈ సర్క్యూట్ యొక్క, శాఖల ప్రవాహాలు I1
మరియు నేను2.
తెలియదు
ప్రవాహాలు
I3,
I4,
I5,
I6.

నిర్ణయించడం
వ్యవస్థ, మనకు లభిస్తుంది: I3
= 13.75 mA;
I4
= -3.75mA;
I5
= 6.25mA;
I6
= 16.25mA.
ప్రాథమిక భావనలు
ఒక క్లోజ్డ్ సర్క్యూట్ ఎలక్ట్రాన్లను సర్క్యూట్లో అధిక సంభావ్యత నుండి తక్కువ ఒకదానికి తరలించడానికి అనుమతించినప్పుడు విద్యుత్ ప్రవాహం ప్రవహిస్తుంది. మరో మాటలో చెప్పాలంటే, కరెంట్కు ఎలక్ట్రాన్ల మూలం అవసరం, అది వాటిని మోషన్లో అమర్చడానికి శక్తిని కలిగి ఉంటుంది, అలాగే ప్రతికూల ఛార్జీలను తిరిగి ఇచ్చే పాయింట్, ఇది వాటి లోపం ద్వారా వర్గీకరించబడుతుంది. భౌతిక దృగ్విషయంగా, సర్క్యూట్లోని కరెంట్ మూడు ప్రాథమిక పరిమాణాల ద్వారా వర్గీకరించబడుతుంది:
- వోల్టేజ్;
- ప్రస్తుత బలం;
- ఎలక్ట్రాన్లు కదిలే కండక్టర్ యొక్క ప్రతిఘటన.
బలం మరియు ఉద్రిక్తత
ప్రస్తుత బలం (I, ఆంపియర్స్లో కొలుస్తారు) అనేది యూనిట్ సమయానికి సర్క్యూట్లోని ఒక ప్రదేశంలో కదులుతున్న ఎలక్ట్రాన్ల (ఛార్జ్) వాల్యూమ్.మరో మాటలో చెప్పాలంటే, కొలత I అనేది చలనంలో ఉన్న ఎలక్ట్రాన్ల సంఖ్యను నిర్ణయించడం
ఈ పదం కదలికను మాత్రమే సూచిస్తుందని అర్థం చేసుకోవడం చాలా ముఖ్యం: స్టాటిక్ ఛార్జీలు, ఉదాహరణకు, కనెక్ట్ చేయని బ్యాటరీ యొక్క టెర్మినల్స్పై, I యొక్క కొలవదగిన విలువను కలిగి ఉండవు. ఒక దిశలో ప్రవహించే కరెంట్ను డైరెక్ట్ (DC) అంటారు, మరియు కాలానుగుణంగా మారుతున్న దిశను ఆల్టర్నేటింగ్ (AC) అంటారు. వోల్టేజీని పీడనం వంటి దృగ్విషయం ద్వారా లేదా గురుత్వాకర్షణ ప్రభావంతో వస్తువుల సంభావ్య శక్తిలో వ్యత్యాసంగా వివరించవచ్చు.
ఈ అసమతుల్యతను సృష్టించడానికి, మీరు మొదట శక్తిని ఖర్చు చేయాలి, ఇది తగిన పరిస్థితులలో చలనంలో గ్రహించబడుతుంది. ఉదాహరణకు, ఎత్తు నుండి లోడ్ పడిపోయినప్పుడు, దానిని ఎత్తే పని జరుగుతుంది, గాల్వానిక్ బ్యాటరీలలో, రసాయన శక్తిని మార్చడం వల్ల టెర్మినల్స్ వద్ద సంభావ్య వ్యత్యాసం ఏర్పడుతుంది, జనరేటర్లలో - బహిర్గతం ఫలితంగా ఒక విద్యుదయస్కాంత క్షేత్రం
ఒత్తిడిని పీడనం వంటి దృగ్విషయం ద్వారా లేదా గురుత్వాకర్షణ ప్రభావంతో వస్తువుల సంభావ్య శక్తిలో వ్యత్యాసంగా వివరించవచ్చు. ఈ అసమతుల్యతను సృష్టించడానికి, మీరు మొదట శక్తిని ఖర్చు చేయాలి, ఇది తగిన పరిస్థితులలో చలనంలో గ్రహించబడుతుంది. ఉదాహరణకు, ఎత్తు నుండి లోడ్ పడిపోయినప్పుడు, దానిని ఎత్తే పని గ్రహించబడుతుంది, గాల్వానిక్ బ్యాటరీలలో రసాయన శక్తిని మార్చడం వల్ల టెర్మినల్స్ వద్ద సంభావ్య వ్యత్యాసం ఏర్పడుతుంది, జనరేటర్లలో - ఒక ఎక్స్పోజర్ ఫలితంగా విద్యుదయస్కాంత క్షేత్రం.
కండక్టర్ నిరోధకత
సాధారణ కండక్టర్ ఎంత మంచిదైనా, ఎలక్ట్రాన్లు వాటి కదలికకు కొంత నిరోధకత లేకుండా వాటిని దాటడానికి అనుమతించదు.ప్రతిఘటనను యాంత్రిక రాపిడి యొక్క అనలాగ్గా పరిగణించడం సాధ్యపడుతుంది, అయితే ఈ పోలిక పరిపూర్ణంగా ఉండదు. కండక్టర్ ద్వారా కరెంట్ ప్రవహించినప్పుడు, కొంత సంభావ్య వ్యత్యాసం వేడిగా మార్చబడుతుంది, కాబట్టి నిరోధకం అంతటా ఎల్లప్పుడూ వోల్టేజ్ డ్రాప్ ఉంటుంది. ఎలక్ట్రిక్ హీటర్లు, హెయిర్ డ్రైయర్లు మరియు ఇతర సారూప్య పరికరాలు వేడి రూపంలో విద్యుత్ శక్తిని వెదజల్లడానికి మాత్రమే రూపొందించబడ్డాయి.
సరళీకృత ప్రతిఘటన (R గా సూచించబడుతుంది) అనేది సర్క్యూట్లో ఎలక్ట్రాన్ల ప్రవాహం ఎంత రిటార్డెడ్ అవుతుందో కొలవడం. ఇది ఓంలలో కొలుస్తారు. రెసిస్టర్ లేదా ఇతర మూలకం యొక్క వాహకత రెండు లక్షణాల ద్వారా నిర్ణయించబడుతుంది:
- జ్యామితి;
- పదార్థం.
హైడ్రాలిక్ సారూప్యత నుండి స్పష్టంగా కనిపించే విధంగా ఆకారం చాలా ముఖ్యమైనది: పొడవాటి మరియు ఇరుకైన పైపు ద్వారా నీటిని నెట్టడం చిన్న మరియు వెడల్పు ద్వారా నీటిని నెట్టడం కంటే చాలా కష్టం. పదార్థాలు నిర్ణయాత్మక పాత్ర పోషిస్తాయి. ఉదాహరణకు, ఎలక్ట్రాన్లు రాగి తీగలో స్వేచ్ఛగా కదలగలవు, కానీ వాటి ఆకారంతో సంబంధం లేకుండా రబ్బరు వంటి అవాహకాల ద్వారా ప్రవహించలేవు. జ్యామితి మరియు పదార్థంతో పాటు, వాహకతను ప్రభావితం చేసే ఇతర అంశాలు కూడా ఉన్నాయి.
ఓం యొక్క చట్టం యొక్క వివరణ
ఛార్జీల కదలికను నిర్ధారించడానికి, మీరు సర్క్యూట్ను మూసివేయాలి. అదనపు శక్తి లేనప్పుడు, కరెంట్ ఎక్కువ కాలం ఉండదు. సంభావ్యత త్వరగా సమానంగా మారుతుంది. సర్క్యూట్ యొక్క ఆపరేటింగ్ మోడ్ను నిర్వహించడానికి, అదనపు మూలం (జనరేటర్, బ్యాటరీ) అవసరం.
పూర్తి సర్క్యూట్ అన్ని భాగాల మొత్తం విద్యుత్ నిరోధకతను కలిగి ఉంటుంది. ఖచ్చితమైన గణనల కోసం, కండక్టర్లలో నష్టాలు, నిరోధక అంశాలు మరియు విద్యుత్ వనరు పరిగణనలోకి తీసుకోబడతాయి.
నిర్దిష్ట కరెంట్ బలం కోసం ఎంత వోల్టేజ్ దరఖాస్తు చేయాలి అనేది సూత్రం ద్వారా లెక్కించబడుతుంది:
U=I*R.
అదేవిధంగా, పరిగణించబడిన సంబంధాల సహాయంతో, సర్క్యూట్ యొక్క ఇతర పారామితులు నిర్ణయించబడతాయి.
సమాంతర మరియు సీరియల్ కనెక్షన్
ఎలెక్ట్రిక్స్లో, మూలకాలు శ్రేణిలో - ఒకదాని తర్వాత ఒకటి లేదా సమాంతరంగా - అనేక ఇన్పుట్లు ఒక బిందువుకు కనెక్ట్ చేయబడినప్పుడు మరియు అదే మూలకాల నుండి అవుట్పుట్లు మరొకదానికి అనుసంధానించబడినప్పుడు.
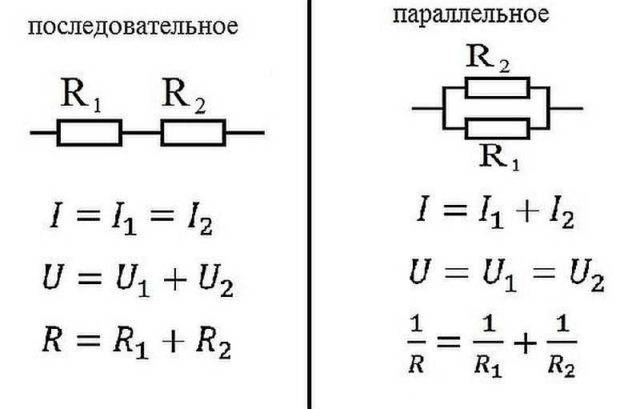
సమాంతర మరియు శ్రేణి కనెక్షన్ కోసం ఓం యొక్క చట్టం
సీరియల్ కనెక్షన్
ఈ కేసులకు ఓం చట్టం ఎలా పని చేస్తుంది? శ్రేణిలో అనుసంధానించబడినప్పుడు, మూలకాల గొలుసు ద్వారా ప్రవహించే కరెంట్ ఒకే విధంగా ఉంటుంది. శ్రేణిలో అనుసంధానించబడిన మూలకాలతో సర్క్యూట్ యొక్క విభాగం యొక్క వోల్టేజ్ ప్రతి విభాగంలోని వోల్టేజీల మొత్తంగా లెక్కించబడుతుంది. దీన్ని ఎలా వివరించవచ్చు? ఒక మూలకం ద్వారా విద్యుత్ ప్రవాహం అనేది ఒక భాగం నుండి మరొకదానికి ఛార్జ్ యొక్క భాగాన్ని బదిలీ చేయడం. నా ఉద్దేశ్యం, ఇది కొంత పని. ఈ పని యొక్క పరిమాణం ఉద్రిక్తత. ఇది ఒత్తిడి యొక్క భౌతిక అర్ధం. ఇది స్పష్టంగా ఉంటే, మేము ముందుకు వెళ్తాము.
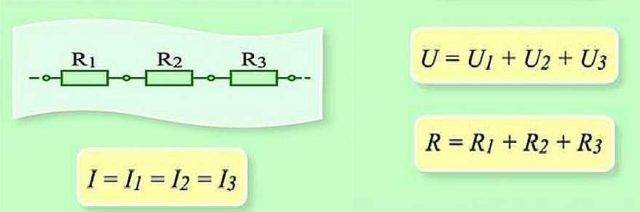
సర్క్యూట్ యొక్క ఈ విభాగం యొక్క సీరియల్ కనెక్షన్ మరియు పారామితులు
సిరీస్లో కనెక్ట్ చేసినప్పుడు, ప్రతి మూలకం ద్వారా ఛార్జ్ను బదిలీ చేయడం అవసరం. మరియు ప్రతి మూలకంపై, ఇది పని యొక్క నిర్దిష్ట "వాల్యూమ్". మరియు గొలుసు యొక్క మొత్తం విభాగంలో పని మొత్తాన్ని కనుగొనడానికి, మీరు ప్రతి మూలకంపై పనిని జోడించాలి. కాబట్టి మొత్తం వోల్టేజ్ అనేది ప్రతి మూలకాలపై వోల్టేజీల మొత్తం అని తేలింది.
అదే విధంగా - అదనంగా సహాయంతో - సర్క్యూట్ విభాగం యొక్క మొత్తం నిరోధకత కూడా కనుగొనబడింది. మీరు దానిని ఎలా ఊహించగలరు? మూలకాల గొలుసు ద్వారా ప్రవహించే కరెంట్ వరుసగా అన్ని ప్రతిఘటనలను అధిగమిస్తుంది. ఒక్కొక్కటిగా. అంటే, అతను అధిగమించిన ప్రతిఘటనను కనుగొనడానికి, ప్రతిఘటనలను జోడించడం అవసరం. ఎక్కువ లేదా తక్కువ ఇలా.గణిత ఉత్పన్నం మరింత క్లిష్టంగా ఉంటుంది మరియు ఈ చట్టం యొక్క ఆపరేషన్ యొక్క యంత్రాంగాన్ని అర్థం చేసుకోవడం సులభం.
సమాంతర కనెక్షన్
కండక్టర్ల / మూలకాల యొక్క ప్రారంభాలు ఒక బిందువు వద్ద కలుస్తాయి మరియు మరొక సమయంలో వాటి చివర్లు అనుసంధానించబడినప్పుడు సమాంతర కనెక్షన్. ఈ రకమైన సమ్మేళనాలకు చెల్లుబాటు అయ్యే చట్టాలను వివరించడానికి మేము ప్రయత్నిస్తాము. కరెంట్తో ప్రారంభిద్దాం. మూలకాల యొక్క కనెక్షన్ పాయింట్కి కొంత పరిమాణంలో కరెంట్ సరఫరా చేయబడుతుంది. ఇది అన్ని కండక్టర్ల ద్వారా ప్రవహిస్తుంది, వేరు చేస్తుంది. దీని నుండి మేము విభాగంలోని మొత్తం కరెంట్ ప్రతి మూలకాలలోని ప్రస్తుత మొత్తానికి సమానం అని నిర్ధారించాము: I = I1 + I2 + I3.
ఇప్పుడు వోల్టేజ్ కోసం. వోల్టేజ్ అనేది ఛార్జ్ని తరలించడానికి పని చేస్తే, ఒక ఛార్జీని తరలించడానికి అవసరమైన పని ఏదైనా మూలకంపై ఒకే విధంగా ఉంటుంది. అంటే, ప్రతి సమాంతరంగా కనెక్ట్ చేయబడిన మూలకంపై వోల్టేజ్ ఒకే విధంగా ఉంటుంది. U=U1=U2=U3. గొలుసు విభాగానికి ఓం యొక్క చట్టం యొక్క వివరణ విషయంలో వలె సరదాగా మరియు దృశ్యమానంగా లేదు, కానీ మీరు అర్థం చేసుకోవచ్చు.
సమాంతర కనెక్షన్ కోసం చట్టాలు
ప్రతిఘటన కోసం, విషయాలు కొంచెం క్లిష్టంగా ఉంటాయి. వాహకత భావనను పరిచయం చేద్దాం. ఈ కండక్టర్ ద్వారా ఛార్జ్ పాస్ చేయడం ఎంత సులభమో లేదా కష్టమో సూచించే లక్షణం. తక్కువ ప్రతిఘటన, కరెంట్ పాస్ చేయడానికి సులభంగా ఉంటుందని స్పష్టమవుతుంది. కాబట్టి, వాహకత - G - ప్రతిఘటన యొక్క పరస్పరంగా లెక్కించబడుతుంది. ఫార్ములాలో, ఇది ఇలా కనిపిస్తుంది: G = 1/R.
మనం వాహకత గురించి ఎందుకు మాట్లాడుతున్నాము? ఎందుకంటే మూలకాల యొక్క సమాంతర అనుసంధానంతో ఒక విభాగం యొక్క మొత్తం వాహకత ప్రతి విభాగానికి వాహకత మొత్తానికి సమానంగా ఉంటుంది. G = G1 + G2 + G3 - అర్థం చేసుకోవడం సులభం. సమాంతర మూలకాల యొక్క ఈ నోడ్ను కరెంట్ ఎంత సులభంగా అధిగమిస్తుంది అనేది ప్రతి మూలకం యొక్క వాహకతపై ఆధారపడి ఉంటుంది. కాబట్టి అవి మడవాల్సిన అవసరం ఉందని తేలింది.
ఇప్పుడు మనం ప్రతిఘటనకు వెళ్లవచ్చు.వాహకత అనేది ప్రతిఘటన యొక్క పరస్పరం కాబట్టి, మేము ఈ క్రింది సూత్రాన్ని పొందవచ్చు: 1/R = 1/R1 + 1/R2 + 1/R3.
మనకు సమాంతర మరియు సీరియల్ కనెక్షన్ని ఏది ఇస్తుంది?
సైద్ధాంతిక జ్ఞానం మంచిది, కానీ ఆచరణలో ఎలా దరఖాస్తు చేయాలి? ఏ రకమైన ఎలిమెంట్స్ అయినా సమాంతరంగా మరియు శ్రేణిలో కనెక్ట్ చేయబడతాయి. కానీ మేము సరళ మూలకాలను వివరించే సరళమైన సూత్రాలను మాత్రమే పరిగణించాము. లీనియర్ ఎలిమెంట్స్ రెసిస్టెన్స్, వీటిని "రెసిస్టర్లు" అని కూడా అంటారు. కాబట్టి మీరు నేర్చుకున్న వాటిని ఎలా ఉపయోగించవచ్చో ఇక్కడ ఉంది:
పెద్ద-విలువ రెసిస్టర్ అందుబాటులో లేనట్లయితే, అనేక చిన్నవి ఉంటే, సిరీస్లో అనేక రెసిస్టర్లను కనెక్ట్ చేయడం ద్వారా కావలసిన ప్రతిఘటనను పొందవచ్చు. మీరు గమనిస్తే, ఇది ఉపయోగకరమైన ట్రిక్.
బ్యాటరీల జీవితాన్ని పొడిగించడానికి, వాటిని సమాంతరంగా కనెక్ట్ చేయవచ్చు. ఈ సందర్భంలో వోల్టేజ్, ఓం యొక్క చట్టం ప్రకారం, అదే విధంగా ఉంటుంది (మల్టీమీటర్తో వోల్టేజ్ని కొలవడం ద్వారా మీరు నిర్ధారించుకోవచ్చు). మరియు ద్వంద్వ బ్యాటరీ యొక్క "జీవితకాలం" ఒకదానికొకటి భర్తీ చేసే రెండు మూలకాల కంటే చాలా పొడవుగా ఉంటుంది
కేవలం గమనించండి: ఒకే సంభావ్యత కలిగిన విద్యుత్ సరఫరాలను మాత్రమే సమాంతరంగా కనెక్ట్ చేయవచ్చు. అంటే, చనిపోయిన మరియు కొత్త బ్యాటరీని కనెక్ట్ చేయడం సాధ్యం కాదు.
మీరు ఇప్పటికీ కనెక్ట్ చేసినట్లయితే, పెద్ద ఛార్జ్ ఉన్న బ్యాటరీ తక్కువ ఛార్జ్ చేయబడిన బ్యాటరీని ఛార్జ్ చేస్తుంది. ఫలితంగా, వారి మొత్తం ఛార్జ్ తక్కువ విలువకు పడిపోతుంది.
సాధారణంగా, ఈ సమ్మేళనాలకు ఇవి అత్యంత సాధారణ ఉపయోగాలు.
ఆదర్శ EMF మూలం
ఎలక్ట్రోమోటివ్ ఫోర్స్ (E) అనేది ఛార్జ్ క్యారియర్ల క్లోజ్డ్ సర్క్యూట్లో కదలికపై బాహ్య శక్తుల ప్రభావం యొక్క డిగ్రీని నిర్ణయించే భౌతిక పరిమాణం. మరో మాటలో చెప్పాలంటే, కండక్టర్ ద్వారా కరెంట్ ఎంత బలంగా ప్రవహిస్తుంది అనేది EMFపై ఆధారపడి ఉంటుంది.
అటువంటి అపారమయిన దృగ్విషయాలను వివరించేటప్పుడు, దేశీయ పాఠశాల ఉపాధ్యాయులు హైడ్రాలిక్ సారూప్యాల పద్ధతికి మారడానికి ఇష్టపడతారు. కండక్టర్ ఒక పైపు అయితే, విద్యుత్ ప్రవాహం దాని ద్వారా ప్రవహించే నీటి మొత్తం, అప్పుడు EMF అనేది పంపు ద్రవాన్ని పంప్ చేయడానికి అభివృద్ధి చేసే ఒత్తిడి.
ఎలక్ట్రోమోటివ్ ఫోర్స్ అనే పదం వోల్టేజ్ వంటి భావనకు సంబంధించినది. ఆమె, EMF, వోల్ట్లలో కూడా కొలుస్తారు (యూనిట్ - "V"). ప్రతి విద్యుత్ వనరు, అది బ్యాటరీ అయినా, జనరేటర్ అయినా లేదా సోలార్ ప్యానెల్ అయినా దాని స్వంత ఎలక్ట్రోమోటివ్ ఫోర్స్ ఉంటుంది. తరచుగా ఈ EMF అవుట్పుట్ వోల్టేజ్ (U)కి దగ్గరగా ఉంటుంది, కానీ ఎల్లప్పుడూ దాని కంటే కొంచెం తక్కువగా ఉంటుంది. ఇది మూలం యొక్క అంతర్గత ప్రతిఘటన వలన సంభవిస్తుంది, వోల్టేజ్ యొక్క భాగం అనివార్యంగా పడిపోతుంది.
ఈ కారణంగా, EMF యొక్క ఆదర్శ మూలం ఒక వియుక్త భావన లేదా వాస్తవ ప్రపంచంలో చోటు లేని భౌతిక నమూనా, ఎందుకంటే బ్యాటరీ రిన్ యొక్క అంతర్గత నిరోధం చాలా తక్కువగా ఉన్నప్పటికీ, ఇప్పటికీ సంపూర్ణ సున్నా నుండి భిన్నంగా ఉంటుంది.
emf యొక్క ఆదర్శ మరియు నిజమైన మూలం
అవకలన రూపంలో
సూత్రం చాలా తరచుగా అవకలన రూపంలో ప్రదర్శించబడుతుంది, ఎందుకంటే కండక్టర్ సాధారణంగా అసమానంగా ఉంటుంది మరియు దానిని సాధ్యమైనంత చిన్న విభాగాలుగా విభజించడం అవసరం. దాని గుండా వెళుతున్న కరెంట్ పరిమాణం మరియు దిశతో ముడిపడి ఉంటుంది, కాబట్టి ఇది స్కేలార్ పరిమాణంగా పరిగణించబడుతుంది. తీగ ద్వారా వచ్చే కరెంట్ని గుర్తించినప్పుడల్లా, అన్ని వ్యక్తిగత ప్రవాహాల బీజగణిత మొత్తం తీసుకోబడుతుంది. ఈ నియమం స్కేలార్ పరిమాణాలకు మాత్రమే వర్తిస్తుంది కాబట్టి, కరెంట్ కూడా స్కేలార్ పరిమాణంగా తీసుకోబడుతుంది. ప్రస్తుత dI = jdS విభాగం గుండా వెళుతుందని తెలుసు. దానిపై వోల్టేజ్ Edl, అప్పుడు స్థిరమైన క్రాస్ సెక్షన్ మరియు సమాన పొడవు ఉన్న వైర్ కోసం, నిష్పత్తి నిజం అవుతుంది:
 అవకలన రూపం
అవకలన రూపం
కాబట్టి, వెక్టర్ రూపంలో కరెంట్ యొక్క వ్యక్తీకరణ ఇలా ఉంటుంది: j = E.
ముఖ్యమైనది! లోహ కండక్టర్ల విషయంలో, పెరుగుతున్న ఉష్ణోగ్రతతో వాహకత తగ్గుతుంది, సెమీకండక్టర్లకు ఇది పెరుగుతుంది. ఓమోవ్ చట్టం కఠినమైన అనుపాతతను ప్రదర్శించలేదు
లోహాలు మరియు మిశ్రమాల యొక్క పెద్ద సమూహం యొక్క ప్రతిఘటన సంపూర్ణ సున్నాకి దగ్గరగా ఉన్న ఉష్ణోగ్రత వద్ద అదృశ్యమవుతుంది మరియు ఈ ప్రక్రియను సూపర్ కండక్టివిటీ అంటారు.